Wie Fibonacci-Zahlen entstehen
Die Fibonacci-Zahlen bilden eine Folge von Zahlen, deren Entstehung man recht gut mit der folgenden Aufgabe versteht:
Leonardo da Pisa, genannt Fibonacci (etwa 1170-1250), schrieb um 1202 ein Buch mit Rechenaufgaben,
das «Liber Abbaci» (lat. liber=Buch, abacus=Rechenbrett). Darin gibt es eine Kaninchenaufgabe:
Ein Mann hält sich ein Kaninchenpärchen in einem Gehege. Dieses Kaninchenpaar bekommt jeden Monat Nachwuchs,
aber erst vom 2. Lebensmonat an (also im 1. Lebensmonat noch nicht, das ist wichtig!).
Der Nachwuchs besteht immer aus zwei Kaninchenkindern, und zwar immer aus einem Männchen und einem Weibchen (ein neues Pärchen).
Die Kinder verhalten sich genauso wie ihre Eltern, bekommen also im ersten Monat noch keine Kinder, danach aber Monat für Monat zwei Kinder
in Form eines neuen Pärchens.
Wie viele Kaninchenpaare gibt es dann nach 12 Monaten?
Lösung:
- Nach 1 Monat gibt es immer noch 1 Paar, weil es erst ab dem 2. Lebensmonat Nachwuchs gibt.
- Nach 2 Monaten hat das Pärchen Junge bekommen, es gibt 2 Pärchen.
- Nach 3 Monaten hat das erste Pärchen nochmal Junge bekommen, das zweite noch nicht, es dauert ja
einen Monat, bis sie Junge bekommen, also 3 Pärchen.
- Nach 4 Monaten gibt es von den ersten beiden Pärchen Junge, also 3+2=5 Pärchen.
- Nach 5 Monaten haben die Pärchen nochmal Junge bekommen, die schon vor 2 Monaten da waren, also
sind es jetzt 5+3=8 Pärchen.
| Am Anfang | 1 Paar |
| Nach 1 Monat | 1 Paar |
| Nach 2 Monaten | 1+1=2 Paare |
| Nach 3 Monaten | 2+1=3 Paare |
| Nach 4 Monaten | 3+2=5 Paare |
| Nach 5 Monaten | 5+3=8 Paare |
| Nach 6 Monaten | 8+5=13 Paare |
| Nach 7 Monaten | 13+8=21 Paare |
| Nach 8 Monaten | 21+13=34 Paare |
| Nach 9 Monaten | 34+21=55 Paare |
| Nach 10 Monaten | 55+34=89 Paare |
| Nach 11 Monaten | 89+55=144 Paare |
| Nach 12 Monaten | 144+89=233 Paare |
Nach 12 Monaten sind es schon 233 Paare,
also 466 einzelne Kaninchen (s. rechts)!
Die Anzahl der Paare an den Monatsenden
nennt man auch die Fibonacci-Zahlen:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
Und nun zur Fibonacci-Spirale...

Wie eine Fibonacci-Spirale entsteht
 Wenn man Quadrate mit den Seitenlängen der Fibonacci-Zahlen 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 466 usw. so anordnet wie im Schaubild rechts, kann man eine besonders schöne Spirale, die sog. Fibonacci-Spirale darin konstruieren.
Wenn man Quadrate mit den Seitenlängen der Fibonacci-Zahlen 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 466 usw. so anordnet wie im Schaubild rechts, kann man eine besonders schöne Spirale, die sog. Fibonacci-Spirale darin konstruieren.
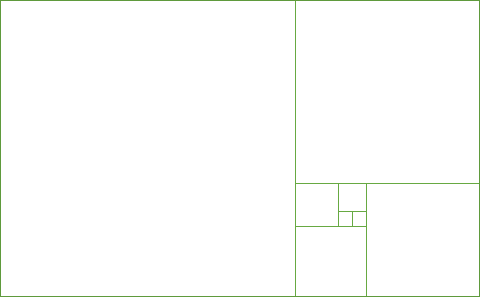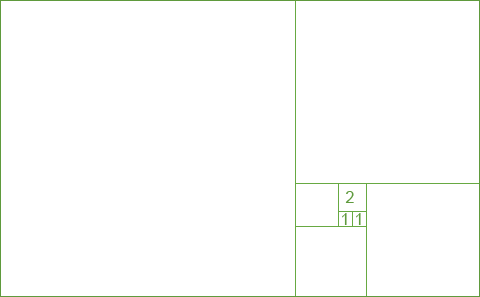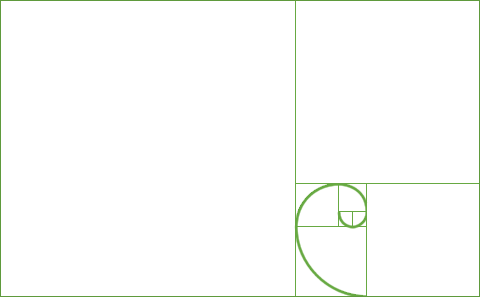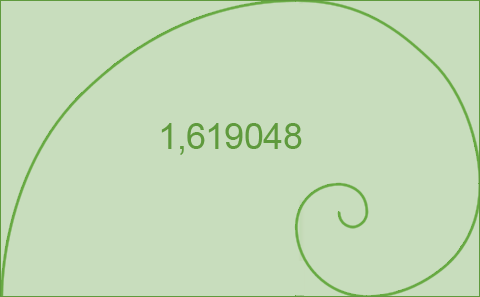
Das Verhältnis der von der Größe her benachbarten Quadrate nähert sich dabei immer mehr dem Verhältnis des «Goldenen Schnittes» an,
einem als besonders harmonisch empfundenen Größenverhältnis, das in der Kunst eine große Rolle spielt.

